迷你蓝牙综测仪

0. 前言

在前一篇文章中，我们用USRP搭了个自打自收传音频的系统。然而在实际产品中，无论是法规、行业标准还是公司内部流程，对通信性能的指标都严格得多，绝对不是能连上就行。接收机的误码率和发射机的功率、调制准确度都有一套完整的测试规范。

要测这些指标自然需要仪表。以测发射机为例，发射机发射一个信号给仪表，仪表采样之后分析得出功率、EVM等指标。USRP刚好也可以做这件事。本文接下来会介绍把USRP做成一台能测蓝牙的综合测试仪。

1. 环境准备

测试模式的ESP32

要把USRP当仪表的话自然需要一个待测物给他测，最好是市面上正在销售的蓝牙产品。虽然手机和电脑都有蓝牙，但是正常工作中的蓝牙会进行每秒1600次的跳频，我们很难固定守在某个信道采样。这些蓝牙设备通常都有一个“测试模式”可以强制发射某个频率的信号，而测试模式需要特定的固件和权限，手机和电脑自然是不会开放给普通消费者的。

刚好我手边又有一块ESP32开发板，可以烧成测试模式的固件然后来测。我这里用的是ESP32，不是ESP32-S3，因为后来出的ESP32-S3为了更贴合物联网的应用，不支持BR/EDR，只支持BLE了。参考ESP的文档[1]，烧录测试模式固件以后就可以测了。

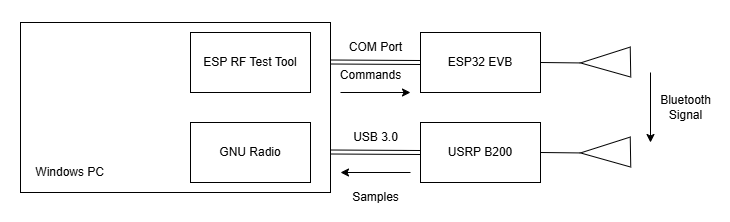
整体测试环境如图： vsa_blockdiagram

Burst检测

经典蓝牙BR/EDR的带宽是1MHz，每次采样都是64位复数（32位实部+32位虚部）的话，每秒会有64M比特，大约8MB的数据量。USB传输和电脑端的处理速度会成为瓶颈。因此不能持续采样，而是只在检测到有信号的时候开始采样，来大幅降低电脑端的处理压力。

我把收到的功率做了滑动平均以后和某个阈值作比较，来判断有没有收到信号。流图中的Burst Tagger检测到Burst以后会打上sob (start of burst)和eob (end of burst)的tag，后续再根据tag转成PDU。

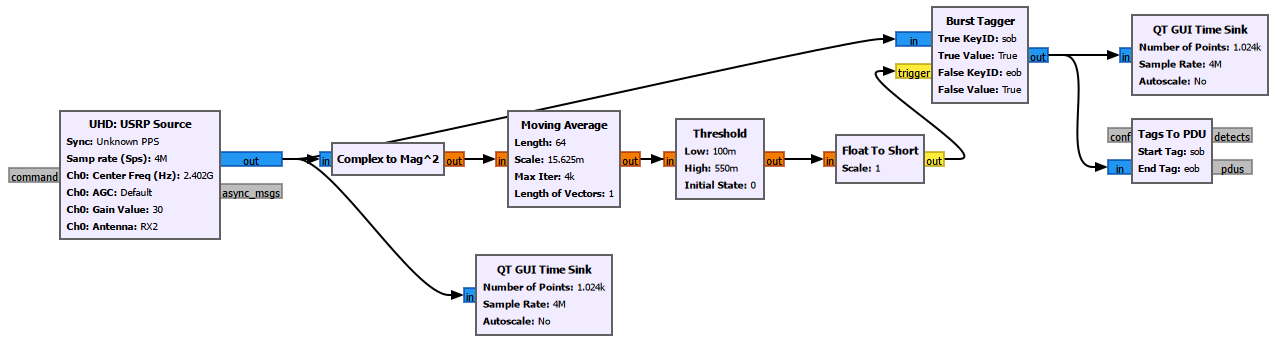
vsa_burst

PDU是GNU Radio的一种特殊数据结构，包括一个dictionary和一串原始采样点。Dictionary用来记录用户想记录的这段数据的各项特性，采样点用来给下游继续分析。PDU的最关键的好处是它是异步的。在普通的流图里面数据是时刻不停地从上游传到下游的，一旦有某个环节的处理速度跟不上就会overflow甚至崩溃。而PDU发布的消息会存在队列里，下游从队列里拿出来分析，如果还是跟不上就丢掉，不会导致崩溃。所以之后我会大量用到PDU，PDU搭配自定义Python模块才能发挥出软件无线电真正的功力。

2. BR/BLE

Delta f1与Delta f2

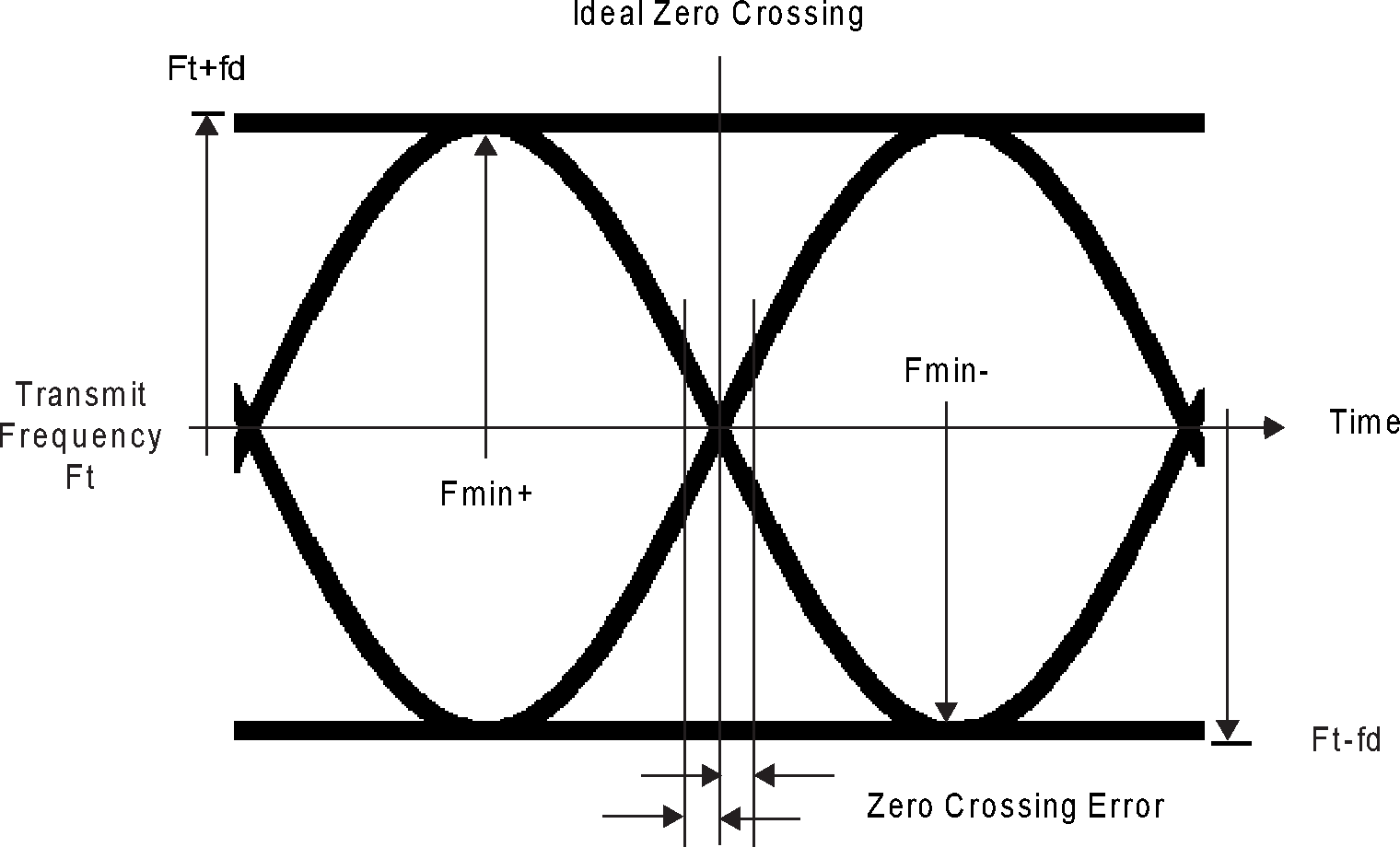
BR/BLE用的是GFSK调制，BT SIG的标准[2]里规定了Frequency Deviation这项指标，即用来表示“0”和用来表示“1”的频率要离得足够远。如图是瞬时频率vs时间，假设Ft是载波频率，Ft+fd用来表示1，Ft-fd用来表示0，那么fd就是我们关心的delta f。当传输的数据是00001111时测的是发射机的平均频偏, 传输10101010测的是发射机在比特切换最快的情况下的瞬时频率响应。BT SIG对二者的上下限都有规定。 vsa_gfsk

解析算法

按照定义来的话，整体思路是

计算瞬时频率 --> 判断当前发送的是否是00001111/10101010序列 --> 计算delta f

瞬时频率可以通过对相位微分来得到。BR的速率是1Mbps，让USRP用4倍采样率即\(f_{s}=4MHz，t_{s}=0.25us\)。每个采样点都包括实部和虚部，所以相位是已知的。从\(n\)时刻到\(n+1\)时刻的相位差可以直接相减，要注意减出来相位有跳变的话要加上\(2\pi\)的整数倍，确保相位差在\((-\pi, \pi)\)的范围。

从\(n-1\)时刻到\(n\)时刻，它们的相位差是

\[\Delta \phi_{n}=\int_{T_{n-1}}^{T_{n}} 2\pi f(t) dt = 2\pi f_{n} t_{s}\]

其中\(f_{n}\)是瞬时频率，\(t_{s}\)是采样间隔。

有了\(f_{n}\)以后，就可以画出瞬时频率vs时间的曲线，再取最近8us内的\(f_{n}\)和理想状况下00001111/10101010对应的曲线做一下correlation，大于某个阈值的话就认为确实收到了这个序列。最后用这8us内的瞬时频率就能计算出delta f。

实验结果

vsa_gfsk_results

实验结果如图。我用让ESP32强发一个BR模式的10101010的序列，然后用GNU Radio的自定义Python Block写了一段程序计算瞬时频率和做correlation。图中的第三幅图就是得到的瞬时频率，最后再算出delta f。

3. EDR

DEVM

蓝牙EDR是蓝牙的一种高速率模式。虽然符号速率仍然是每秒1M个符号，但是通过PSK，一个符号表示2个比特(D-QPSK)或3个比特(D-8PSK)，速率可以达到2Mbps和3Mbps。在PSK和QAM调制中，EVM (Error Vector Magnitude)是个很重要的衡量调制质量的指标。例如在Wi-Fi标准里，EVM的定义是

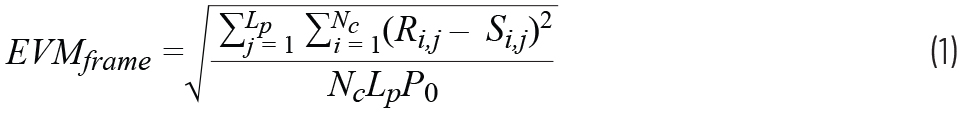
vsa_evm_eq

瞪眼法可以看出来，这个公式里的\(R_{i,j}-S_{i,j}\)是复平面上两个点之间的向量差，更准确地说是实际收到的符号和理想状态下星座图上的符号的向量差。对每个符号都计算差值之后取平均就是整体的EVM。ADI的文档[3]里的这幅图画得很直观，我们最终感兴趣的就是黑色的那个Error Vector的大小。

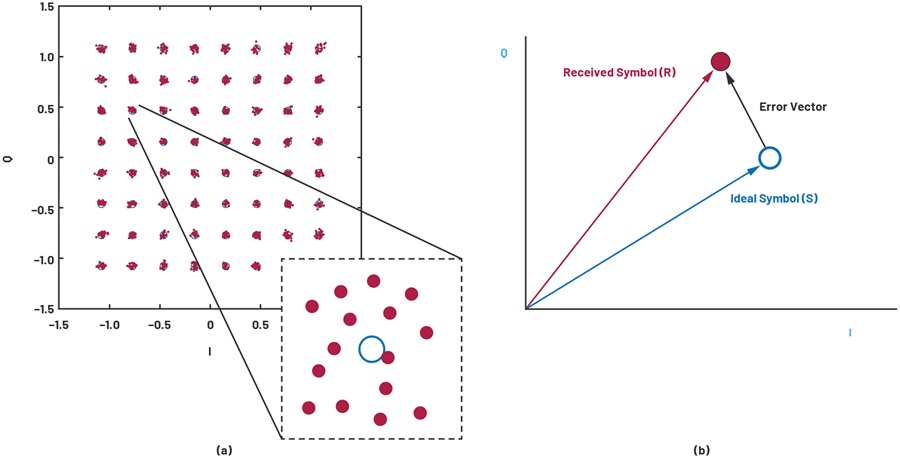
vsa_evm

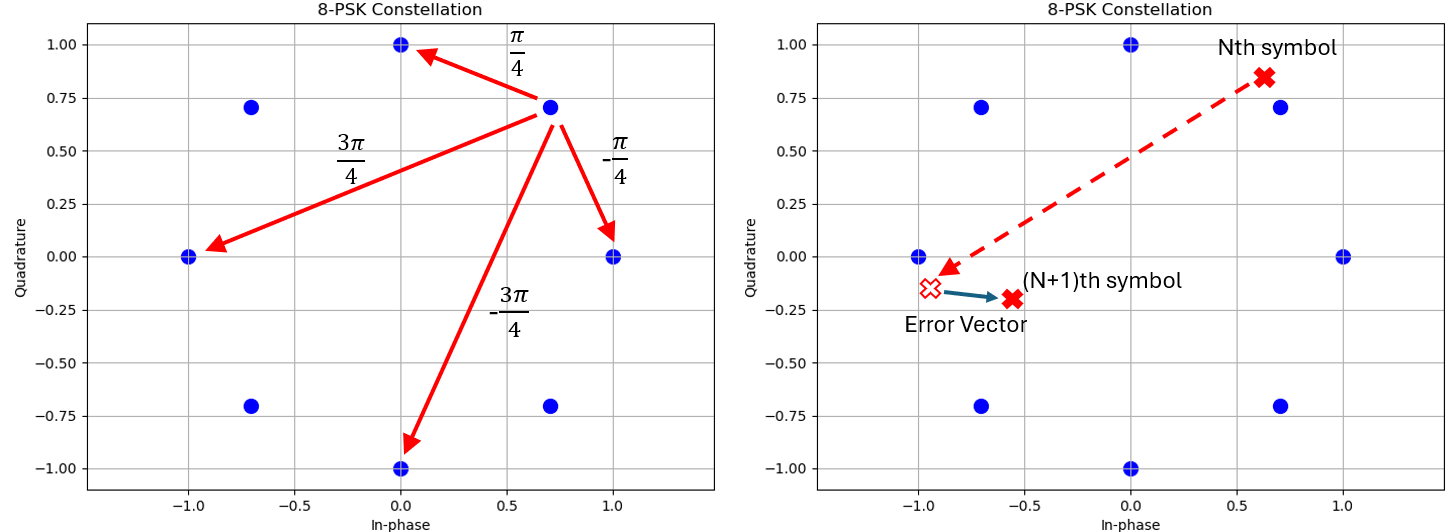
然而，蓝牙EDR用的是差分调制D-QPSK和D-8PSK，我们关心的指标也变成了Diferrential EVM, DEVM，而不是EVM。直觉上说，DEVM的Error Vector要通过两个符号差分得到得到。如图所示，左图表示一个符号点在下一次采样时可能会有\(\frac{\pi}{4}, \frac{3\pi}{4}, -\frac{3\pi}{4}, -\frac{\pi}{4}\)的相位差，分别代表00，01，11，10的数据比特。

接下来在右图，如果我们知道相位差会是\(\frac{3\pi}{4}\)，那么把第N个符号旋转理想的\(\frac{3\pi}{4}\)，再和第N+1个符号作差，得到的就是差分的Error Vector。

vsa_devm

BT SIG的标准[2]里对DEVM有准确的定义，先忽略\(\epsilon,\omega\)的话，和EVM的公式是类似的，也是把Error Vector进行某种平均。我会在附录里介绍\(E_{k}\)和\(Q_{k}\)的准确定义并证明\(E_{k}\)和前面的直觉定义是等价的。

\(\epsilon\)是为了表示在一个符号周期内的哪一个时刻进行采样，\(\omega\)是为了补偿发射机与仪表时钟的差异，也就是在前一篇文章里讲到的会让采样点在星座图上旋转的效应。根据定义，我们需要选择适当的\(\epsilon,\omega\)使DEVM最小。

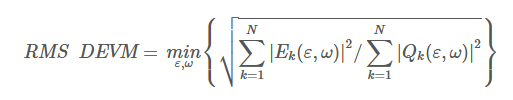
vsa_devm_eq

解析算法

还是按照定义来，整体思路是

信道均衡 --> 截取包的有效部分 --> 载波同步补偿 --> 计算DEVM --> 找到最小值

信道均衡

这部分和做自打自收实验时一样，利用GNU Radio自带的Symbol Sync和Linear Equalizer模块。Costas Loop就不需要了，因为之后会有找关于\(\omega\)的最小值的步骤。要注意2Mbps的EDR用的调制方式虽然叫做D-QPSK，但星座图实际上是和8PSK一样的。[4] [5]

截取包的有效部分

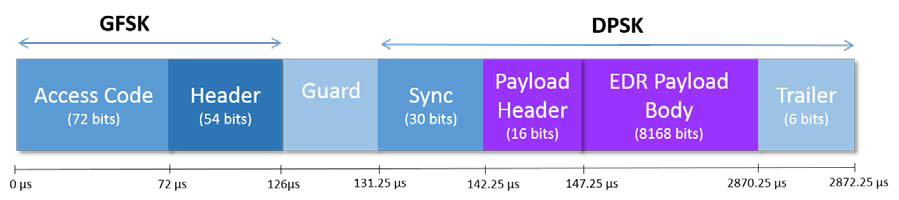
一个EDR包的组成如图所示，其中Access Code和Header用的是GFSK调制，然后会有一个4.75us~5.25us长的Guard Interval，之后才是D-QPSK/D-8PSK的Payload部分。因此，前面的部分不应该拿来计算DEVM，可以直接丢弃，只截取后面的部分。

vsa_edr_packet

载波同步补偿

令\(Z_{n}\)表示原始的第n个符号，那么\(Z^{*}_{n}\)就是补偿过的符号，是把\(Z_{n}\)乘上这段时间里载波偏移产生的相位差，其中\(\omega\)是离散时间的角速度，表示每个采样间隔之间的相位差。

\[Z^{*}_{n}=Z_{n}e^{-j\omega n}\]

代码只要一行：

data_comp = data * np.exp(-1j * w * n)

计算DEVM

按照定义，先算每个符号的Error Vector，再取平均，附录会解释怎样把定义转成更方便算的形式。因为还需要用到“理想状况下两个符号之间的相位差”这个信息，所以代码里先进行了简单的符号判定，\(S_{k}\)用来表示两个符号之间理想的相位差更接近\(\frac{\pi}{4}, \frac{3\pi}{4}, -\frac{3\pi}{4}, -\frac{\pi}{4}\)中的哪个。

DEVM.PACKET_LEN = 50
DEVM.BOUDARIES = np.array([-np.pi, -3*np.pi/4, -np.pi/2, -np.pi/4, 0, np.pi/4, np.pi/2, 3*np.pi/4, np.pi])

phase_diff = np.diff(np.unwrap(np.angle(data_comp)))
phase_diff = np.angle(np.exp(1j * phase_diff))

# Use digitize to find which bin each phase belongs to
# digitize returns 1-based indices, so subtract 1 to get 0-based symbols
symbols = np.digitize(phase_diff, DEVM.BOUDARIES) - 5

# Handle the boundary case at pi (maps to symbol 0)
symbols[symbols == 8] = 0
mapping = np.array([1, 1, 3, 3, -3, -3, -1, -1])

Sk = mapping[symbols] * np.pi /4
for i in range(DEVM.PACKET_LEN):
    Ek2[i] = np.square(np.abs((data_comp[i+1] * np.exp(-1j * Sk[i]) - data_comp[i])))
    Qk2[i] = np.square(np.abs(data_comp[i+1]))

devm = np.sqrt(np.sum(Ek2)/np.sum(Qk2))

找到最小值

接下来需要找到一个合适的\(\omega\)使devm取最小值，当然可以有各种优化算法，但是我这里就用最简单的对\(\omega\)的遍历，效果也不错。

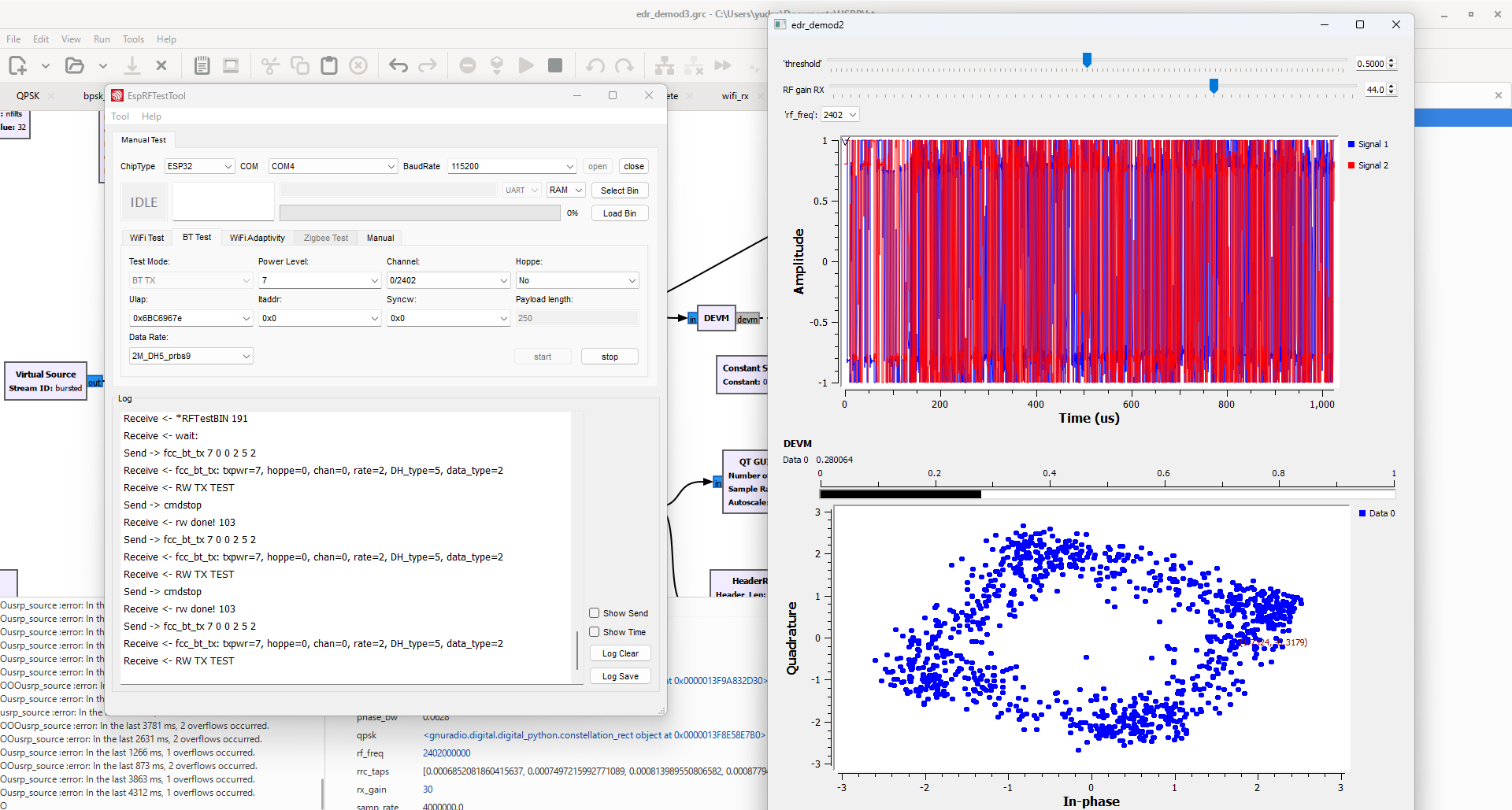
实验结果

最后，我成功解出了DEVM。ESP32发射一个2Mbps，3DH5的PRBS9随机数序列，从时域曲线能看到到130us为止的BPSK的波形和后续波形确实不太一样，所以我只截取后面的来算。从星座图可以看到，因为没有做载波同步，采样点遍布单位圆，并没有形成很集中的8PSK的样子。尽管如此，利用找DEVM关于\(\omega\)的最小值的方法，我们仍然能解出DEVM，并顺便找到了这时的载波偏移\(\omega\)。

vsa_edr_results

4. 结论

本文用USRP实现了一个迷你蓝牙综测仪，可以测试delta f1, delta f2和DEVM。用相同的原理，以后还可以尝试应用到各种其他协议里，比如Zigbee, LoRa, Wi-Fi, GNSS等。

注意，生产环境的要求高得多，要关注仪表自身的噪声、线性度、校准、可靠性、处理速度等非常多的问题。

参考资料

  1. ESP32 RF Test Guide

  2. BR/EDR Controller Radio Specification

  3. How EVM Measurement Improves System Level Performance

  4. QPSK Mod and Demod

  5. M-ASK, M-PSK and QAM-M Mod and Demod

附录 DEVM计算方法

BT Sig的spec原文[2]里有一张框图概括DEVM的计算方法，还有几段话解释了\(Z_{k}\),\(S_{k}\),\(Q_{k}\),\(E_{k}\)分别是什么。简单来说，\(Z_{k}\)是原始采样点，\(S_{k}\)是补偿值，包括载波偏移和理想符号转换，\(Q_{k}\)是补偿后的采样点，\(E_{k}\)是相邻两个\(Q_{k}\)的差。

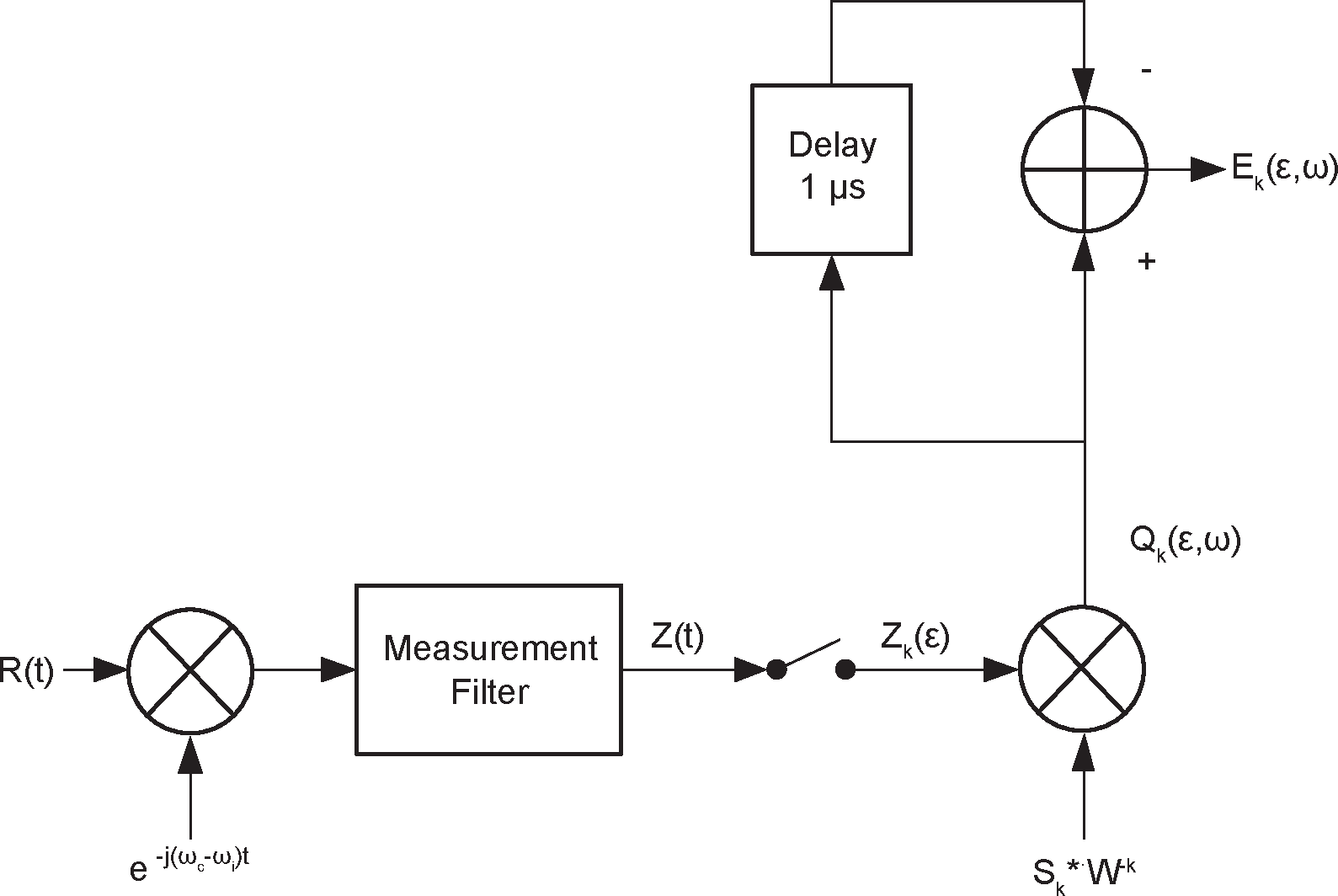
vsa_devm_gen

实际计算中，我需要知道\(||E_{k}||^2\)和\(||Q_{k}||^2\)，假设\(\omega\)已经被补偿掉，于是

\[\begin{split} \begin{aligned} E_{k} &= Q_{k}-Q_{k-1} \\ &= Z_{k}e^{-jS_{k}}-Z_{k-1}e^{-jS_{k-1}} \\ &= e^{-jS_{k}}(Z_{k}-Z_{k-1}e^{S_{k}-S_{k-1}}) \\ &= e^{-jS_{k}}(Z_{k}-Z_{k-1}e^{\Delta S_{k}}) \\ \end{aligned} \end{split}\]
\[||E_{k}||^2 = ||Z_{k}-Z_{k-1}e^{\Delta S_{k}}||^2\]

也就是说\(E_{k}\)的大小就是\(Z_{k-1}\)旋转一定角度之后与\(Z_{k}\)作差。

\(||Q_{k}||^2\)更简单，注意到

\[Q_{k} = Z_{k}e^{-jS_{k}}\]

所以

\[||Q_{k}||^2 = ||Z_{k}||^2\]